DMP part 2: but what about...
Originally posted on my (now-defunct) WordPress blog
I’m back! It’s been a while since the last installment of political nerdery, so I’ll start with a catch-up of some mildly interesting news from the last month. Firstly, a referendum on the voting system in the Canadian province of Prince Edward Island was met with an overwhelming “meh”, with a mixed member proportional system narrowly losing out to the status quo amid abysmal turnout. Ironically enough, if it had been a first-past-the-post election the new system would have won, as it won in more ridings! Thankfully the result wasn’t interpreted as a generational block on any more change, but rather an opportunity for further discussion.
Meanwhile, some local elections happened back home in the UK and highlighted how much of a mess everything is right now. As a maps nerd, I did enjoy following the build up on Election Maps UK, a fun and painstakingly impartial twitter account. I, however, make no claims to impartiality 🔶.
That’s enough current affairs, now it’s time for some DMP. In the last installment of this series (read it now if you haven’t before) I talked about the basic mechanics of this voting system, but now I’m going to look into some of the edge cases, with the help of our good friends in the fictional island nation of Proportionalia. So what about…
…independents?
Independent candidates find it hard enough to break into national elections under FPTP (local elections are a different matter - in the recent English locals, the number of independent councillors increased by 659). Lumping two districts together in DMP just seems like a way to raise the threshold for independents even further.
The benevolent and omnipotent creator of DMP has a solution for this. Like party candidates, independent candidates have two ways to snag a seat: either they win the plurality of votes in a district, or the second most votes in the district. This in turn creates a new problem, in that there are fewer seats to be distributed proportionally, so the initial seat allocation has to be recalculated.
We need to amend the flowchart from the last article to accommodate this detour.
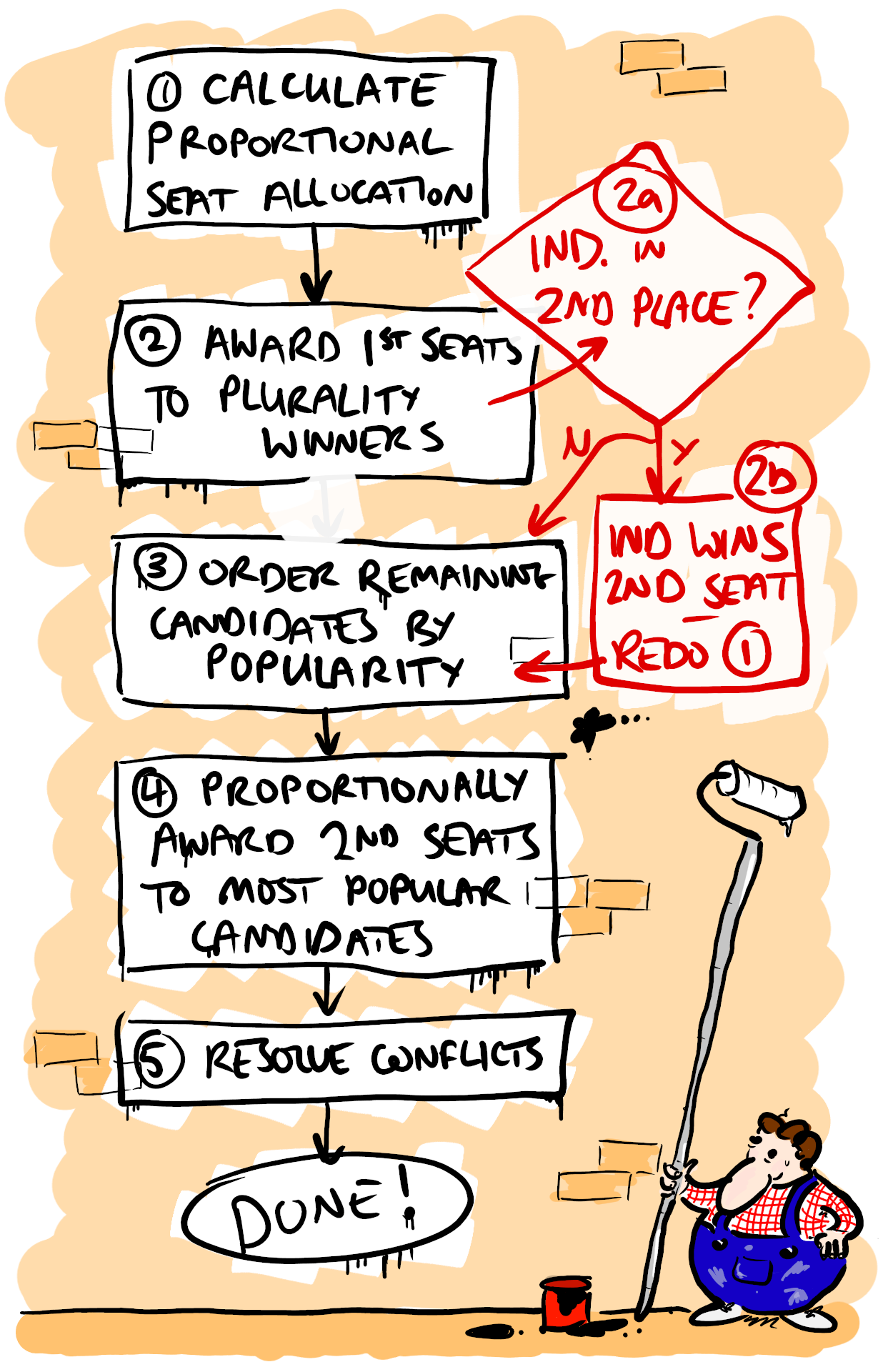
Now in colour!
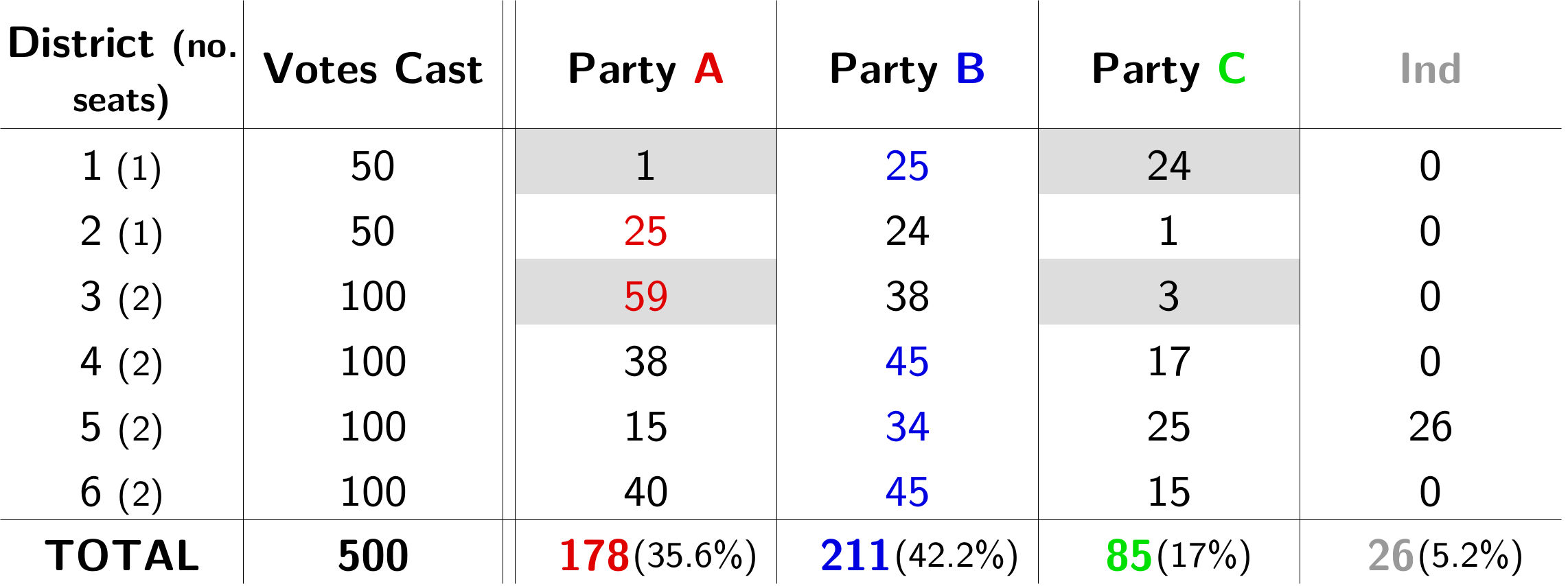
Naturally, an illustrated example will help us get our heads round the change. Let us return to our fictional island nation, Proportionalia. Time has been rewound and the election from part 1 has been rerun. However, this time we throw an independent into the mix (siphoning votes off party B in district 5):
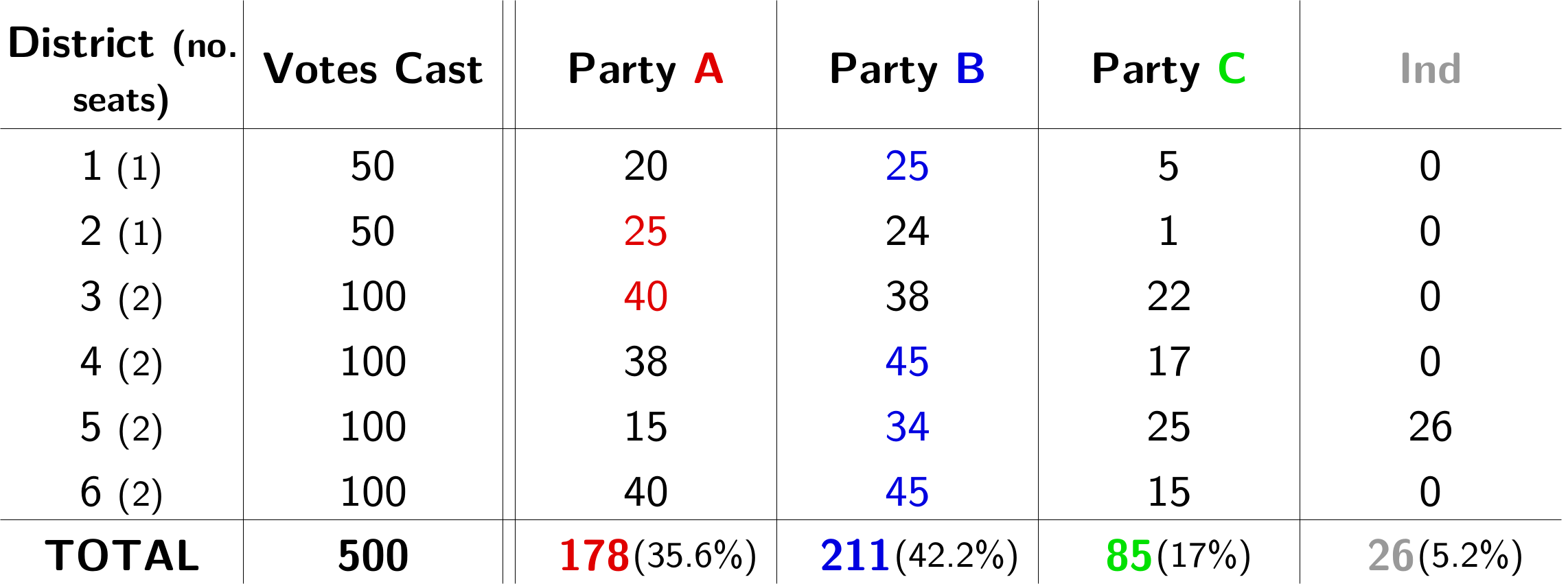
There’s no way I’m going to draw these out by hand again.
Handily enough, the independent vaults into second place in the district, guaranteeing them a seat. This means that the proportional calculations have to be redone with one fewer seat, resulting in this final outcome:
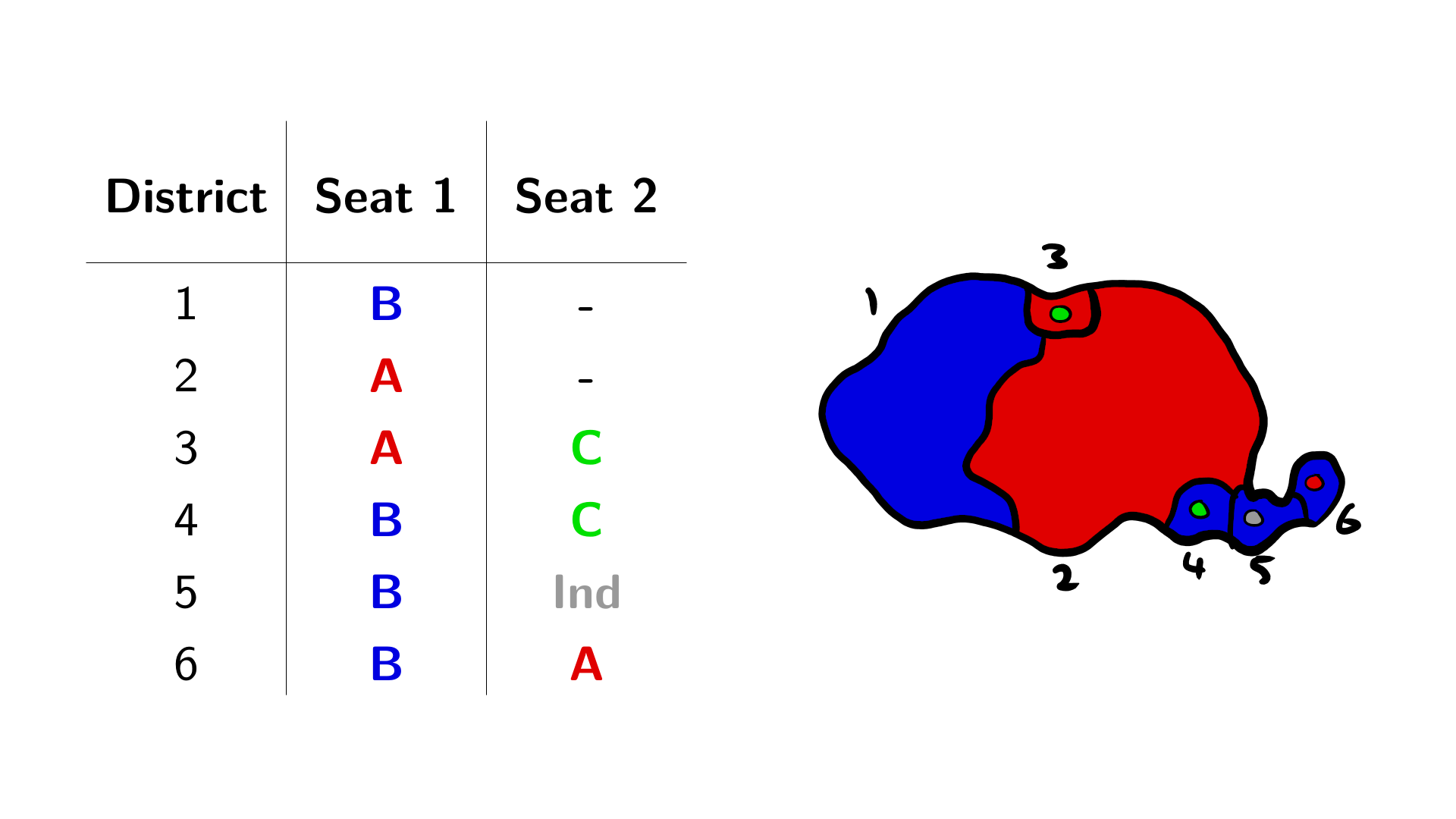
The best thing is that this hardly impacts the overall proportionality - you can work that out for yourself though, I gave Proportionalia 10 seats for a reason.
…really unpopular candidates?
One problem with the algorithm as it stands is that a second seat could, through an unlikely but possible string of conflicts, go to a candidate who received no votes at all! To combat this, a threshold is introduced (typically 5%), below which party candidates are not eligible to take a second seat. For smaller parties, this threshold may lead to the party running out of eligible candidates to fill the seats they are proportionally allocated. Of course, the party may also not have run candidates in some seats as well. In every case where a party cannot fill the number of seats it has been proportionally allocated, it must forfeit them.
The eligibility threshold handily also counteracts the tendency of the LR-Hare proportional representation system to over-represent smaller parties, as these are the ones most likely to forfeit.
So what happens next? At some point when the DMP algorithm is run, the number of unfilled seats will equal the number of seats that have been forfeited. If we’re lucky, that number is zero and we can all go home. If not, the seats that have already been won are now fixed and a new ‘round’ of the algorithm is started only on the unfilled seats, and only with parties that have not forfeited seats. Let’s see what this looks like on our flowchart:
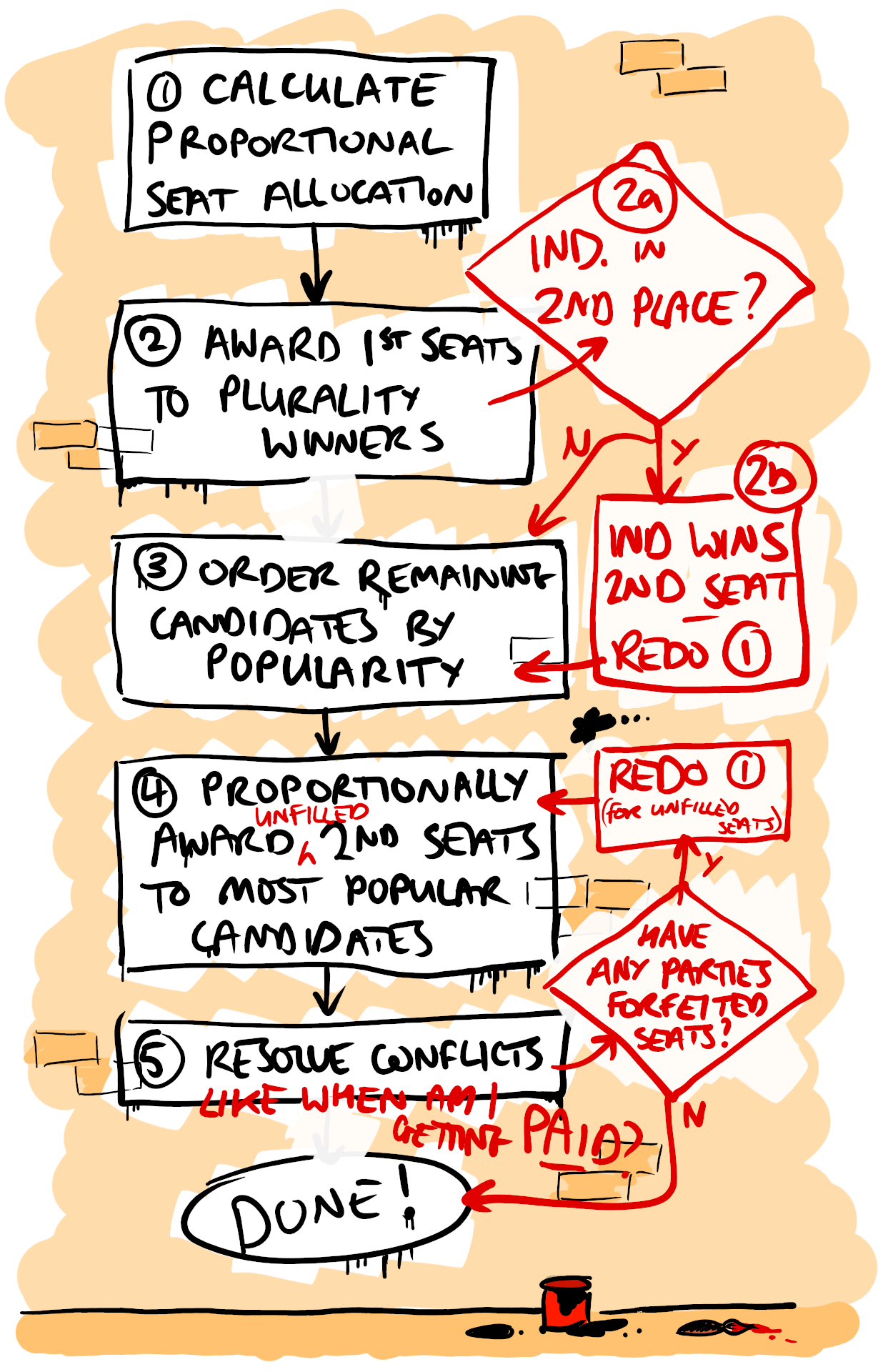
It looks disgusting, that’s what.
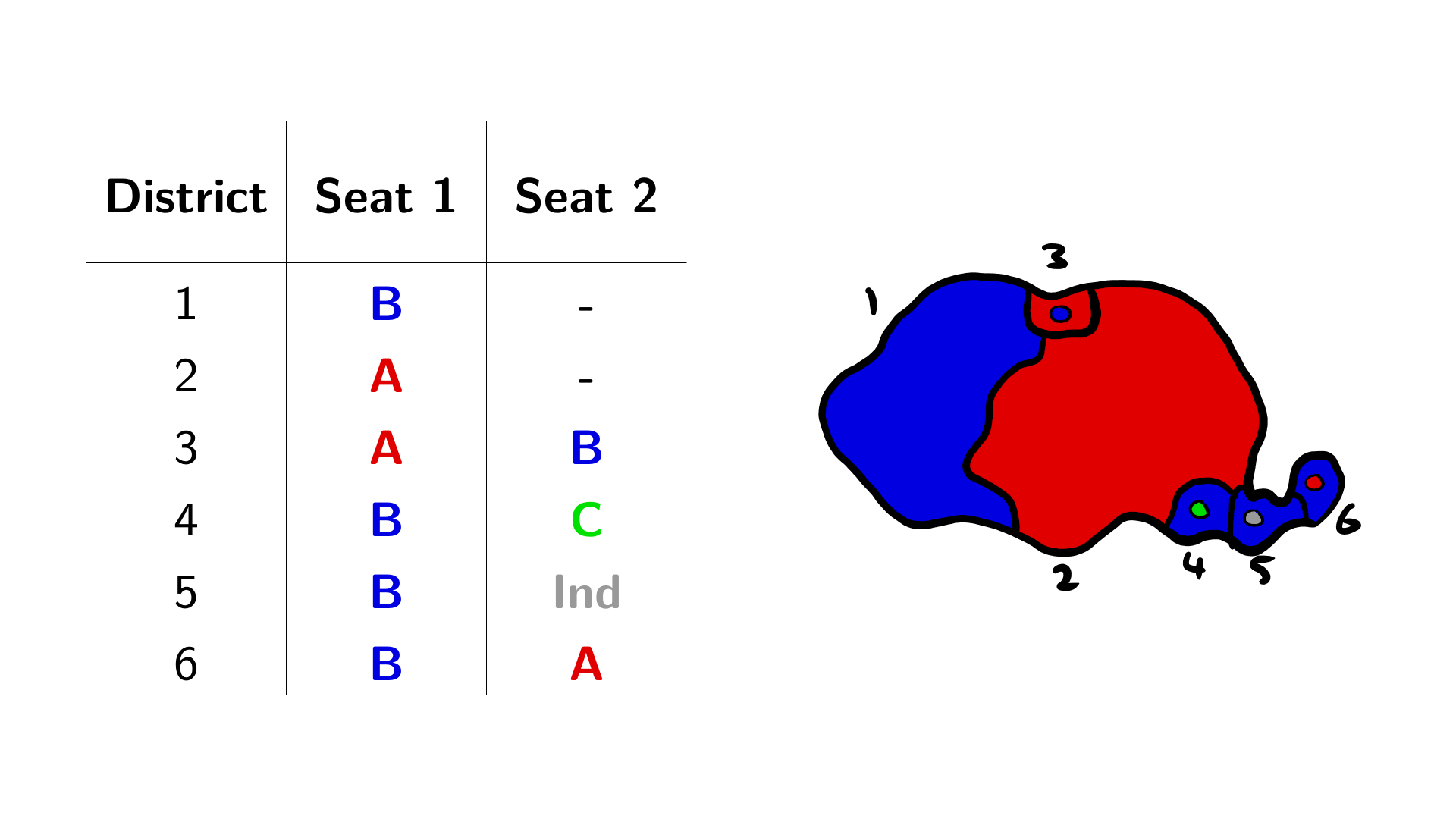
To illustrate this, I’ve tweaked the example from Proportionalia above, being careful to keep the total votes won by each party the same across the island. Why? To keep the proportional seat numbers the same, and also to show how only a few votes moved here and there can create interesting edge cases.
Guess which entries I’ve changed.
As each party’s total vote is unchanged, they are allocated the same number of seats in the proportional scramble. Party C should pick up two second seats, but they only win out in district 4. The independent has already claimed district 5, and party A is too strong in district 6. In the previous example C’s last seat came from district 3, but now they don’t reach the threshold to be eligible and therefore forfeit the seat.
At this stage, a fresh proportional calculation is carried out with all unfilled seats and all remaining (non-forfeiting) parties. As only one seat is available, it simply goes to the most popular party in Proportionalia (B).
All that for a very subtle difference.
…overhang seats?
Sometimes a party will be so annoyingly popular that they’ll win more first seats directly than their proportional allocation. I’ll just plunge straight into an example for this one, with another Proportionalian election slightly different from the one above.
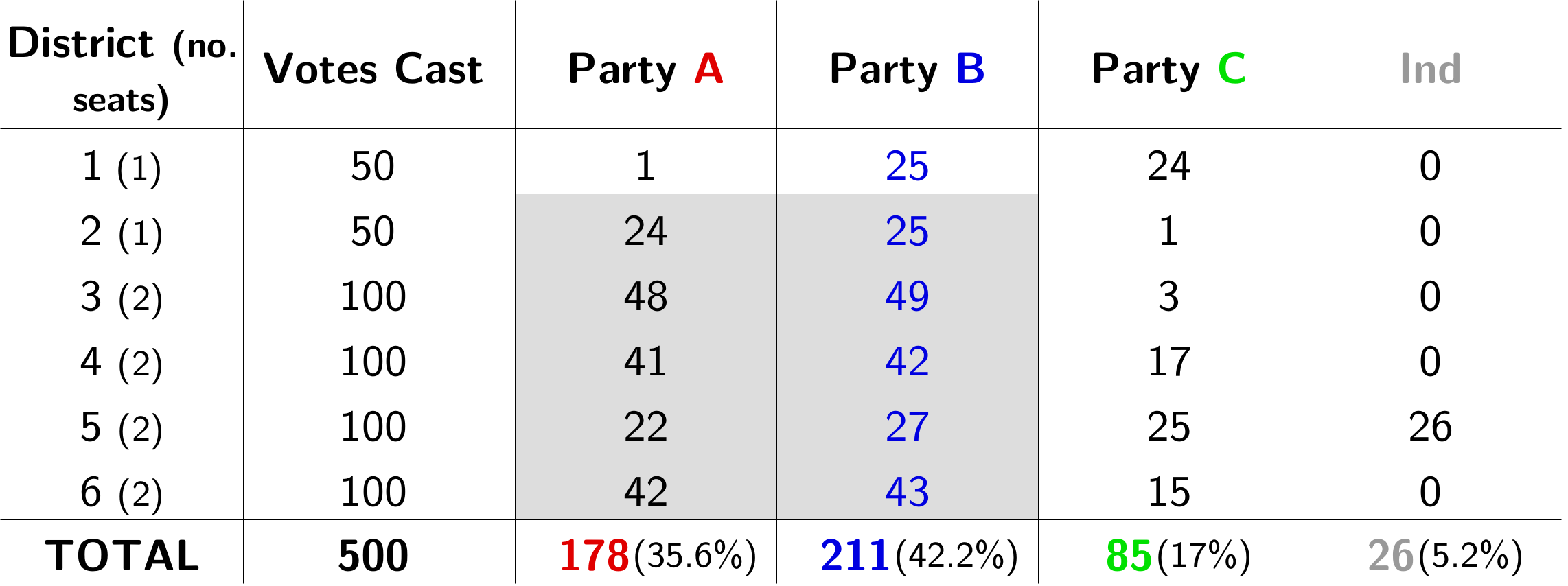
Each of these is getting more and more contrived, but they’re still possible.
Party B has already won 60% of the seats with 42.2% of the vote, before the second seats can even be allocated. In the Mixed Member Proportional (MMP) system, where top-up seats are allocated from a party list instead of fannying around with two-seat districts, these are called ‘overhang seats’. There are two ways to deal with them: the Scottish way and the German way.
The Scottish way is simple. Ignore them. Allocate the top-up seats to the remaining parties as best you can and call it a day. Of course, this means the results can end up being disproportional, as in the Scottish Parliament election of 2011, where the SNP won an overall majority off about 45% of the vote (although the d’Hondt method of calculating the top-up regional seats is also partially to blame).
The German way is a tad braver, as it involves expanding the legislative chamber with more top-up seats to keep the overall result proportional. Cue rabid cries of “Why are we paying for more politicians!?”. The seats that are added to deal with overhangs are called ’leveling seats’, and there can be a lot of them. The Bundestag nominally has 598 members, but after the 2017 election this had to be increased to 709 to maintain proportionality.
Due to the fixed number of seats, DMP has to deal with overhang seats in a more Scottish way. After all the votes have been counted up and the first seats have been won (and second seats won by independents if applicable), it will be evident if any parties are overhanging. Entirely predictably, the next thing to do is recalculate the proportional seat allocations, but this time only for the remaining unfilled seats, and without counting votes for the overhanging party or independents. In this case, there are three seats available to be handed out to parties A and C, who get 2 and 1 respectively (no forfeits in this case).
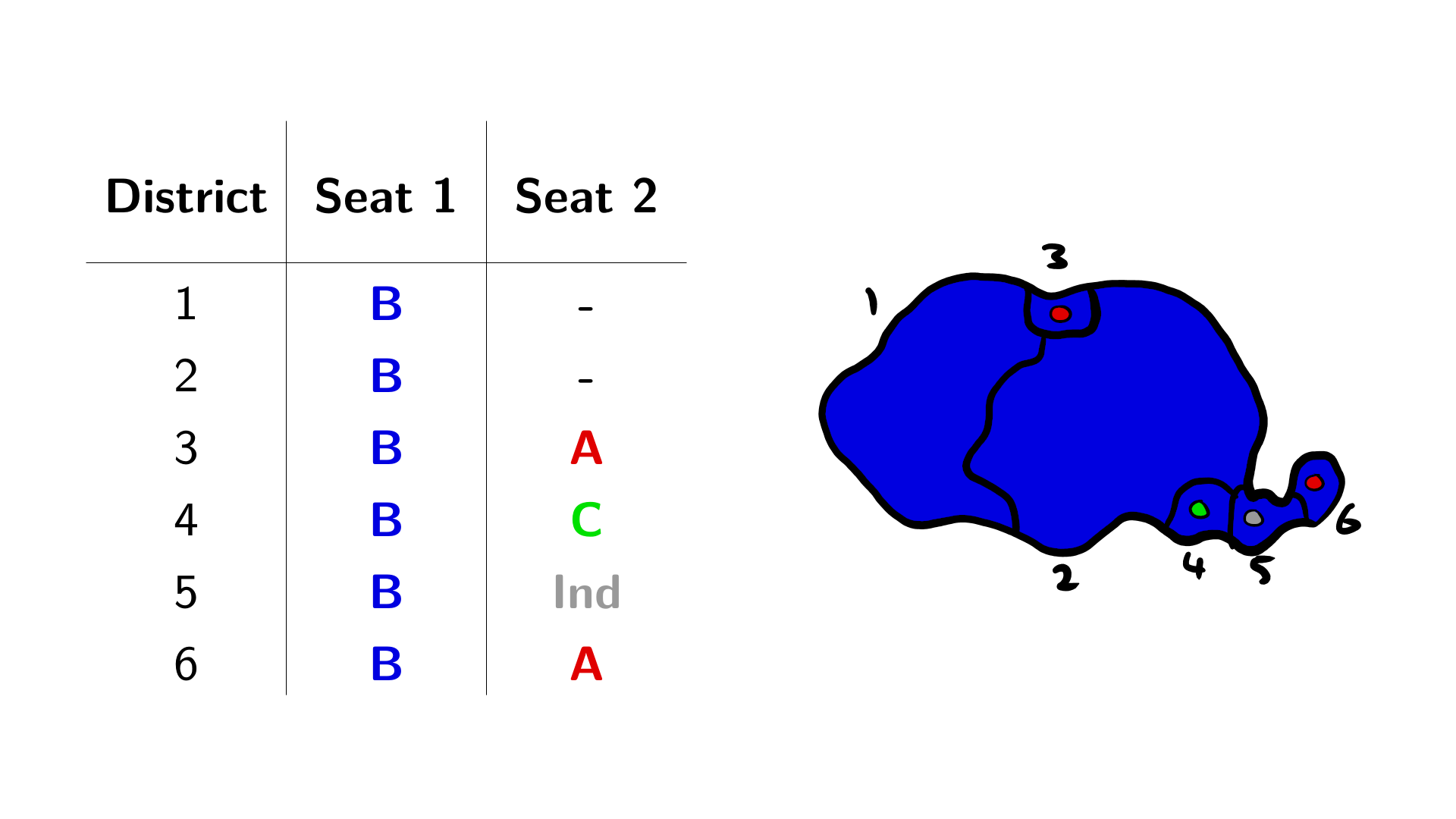
I guess they’re feeling kinda blue…
Let’s see if we can squeeze this onto the wallchart:

What did I do wrong?
…overhang seats AND forfeits?
To be honest, I’m now into pure speculation territory. What’s coming up is just my personal idea of how to deal with this super weird situation. It’s not going on the flowchart without adding another couple of dimensions, and the poor citizens of Proportionalia have been contrived to within an inch of their lives, so you’ve just got to read carefully!
The question is: how do we deal with ’new’ seats freed up by forfeiting parties when we previously had an overhanging party? We don’t want to just include the overhanging party as they’re almost guaranteed to gain even more seats and be even more overhang-y! On the other hand if enough seats are forfeited then excluding a barely overhanging party would result in them ending up with fewer seats than they should compared to other large parties. We need a middle ground.
My solution is to introduce ‘virtual seats’ when deciding how to allocate forfeited seats. That is, if a party had 2 overhang seats at the very first calculation and 5 seats were forfeited by smaller parties, then the proportional redistribution would be calculated for 7 seats. Any seats the overhanging party is allocated would first be checked off against their overhang, then any further ones would be new second seats the party is eligible for.
There. Clear as mud.
…reserve factors?
Hahahahahah nope. I’m not touching this with a 10-foot barge pole, let alone trying to explain it in a semi-understandable way. Readers can look it up themselves if they want.
So what now?
I think we’re all fed up of fictional examples, so in the next installment I’ll be applying a MATLAB script I knocked up (over far too much time) to some real-world examples. At least I think Wales is a real place…