DMP part 1: DMwhat?
Originally posted on my (now-defunct) WordPress blog
Throughout November 2018, British Columbia held a postal referendum on changing the electoral system from our favourite first-past-the-post (FPTP), and one of the options was a system nobody had ever heard of before: DMP, or dual member proportional representation. The people of BC ended up being tricked into voting to keep the status quo for reasons beyond the scope of this blog, but the whole process got me thinking about this mysterious new system. Although the horse has bolted, settled down, raised a family, sent its kids off to college, held its grandchildren and taken a one-way trip to a glue factory in Switzerland, the stable door is still open and it looks untidy.
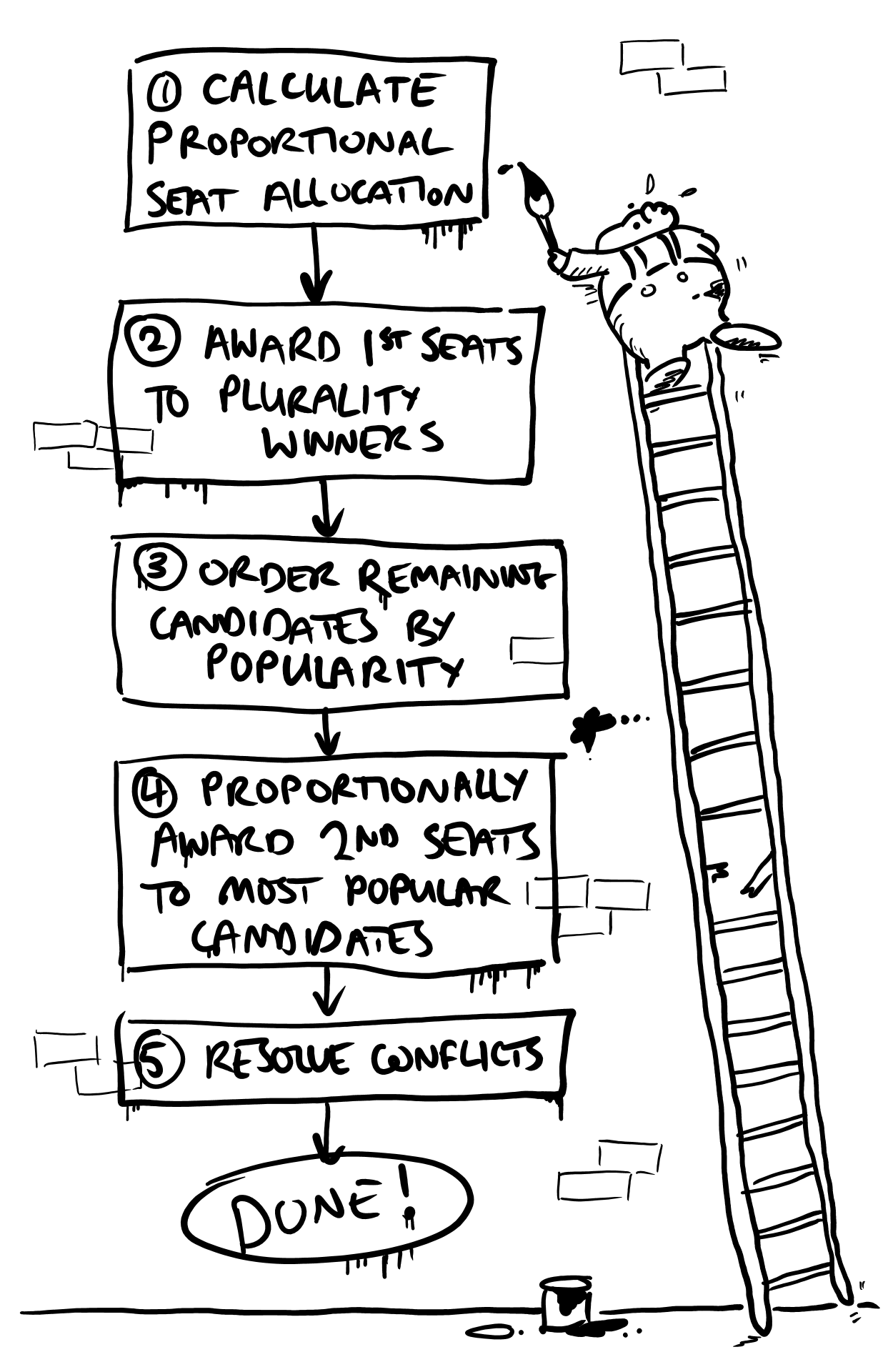
The basic aim behind DMP is to combine the proportionality of… any other proportional system (for example MMP à la Germany and New Zealand) with the ballot simplicity of FPTP (stick a cross in a box). The complexity is then shunted to the counting process; to counteract the disproportionality of the latter system, pairs of districts are combined into one larger district returning two seats. One seat is always allocated to the candidate with the plurality of votes in that district, and the second seat is assigned to another candidate standing in the same district using - brace yourselves - an algorithm. Thankfully, this can all be summarised in a simple flow chart (but don’t worry nerds, it’ll get a lot more complicated in part 2).
Murals are the most cost-effective way to disseminate information

I don’t like Dave Thug, but the nice party can’t win here, so I guess I’ll have to vote for Literally Hitler.
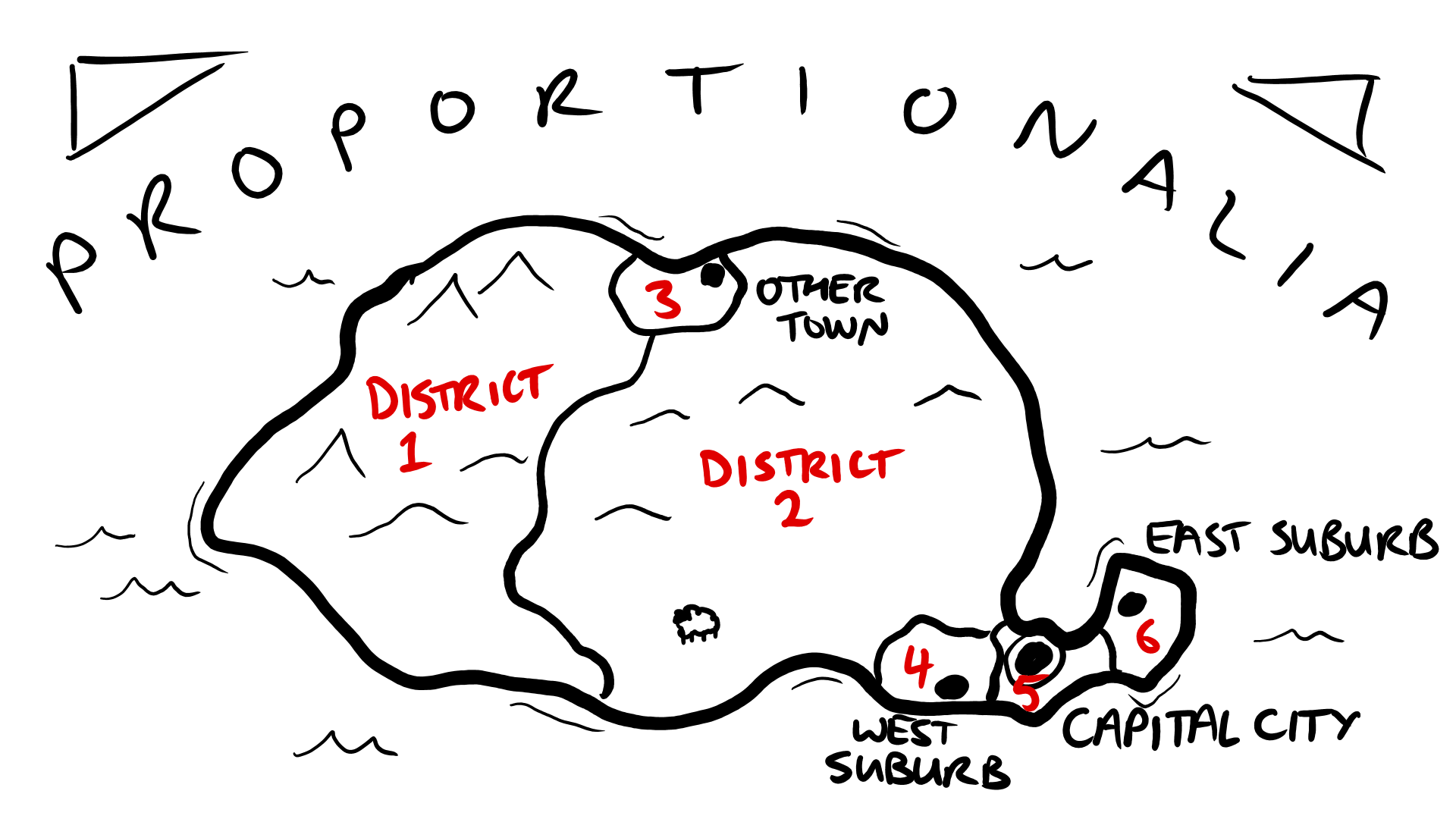
One significant difference between the ballot in DMP and FPTP is that parties may run primary and secondary candidates on the same ticket. If the party directly wins the first seat through plurality, the party vote total is halved and awarded to the secondary candidate, who remains in contention for the second seat. To illustrate the whole process, it’s time for a worked example. Introducing the small island nation of Proportionalia, where people tend to lack imagination in naming things:
Population: one sheep.
Districts 1 and 2 are large and mainly rural, so each of them only returns one representative to ensure local representation. Districts 3-6 are more urban and have a higher population density, so each one has about twice the population and returns two representatives. In the most recent election, the voting breakdown by district is as follows:
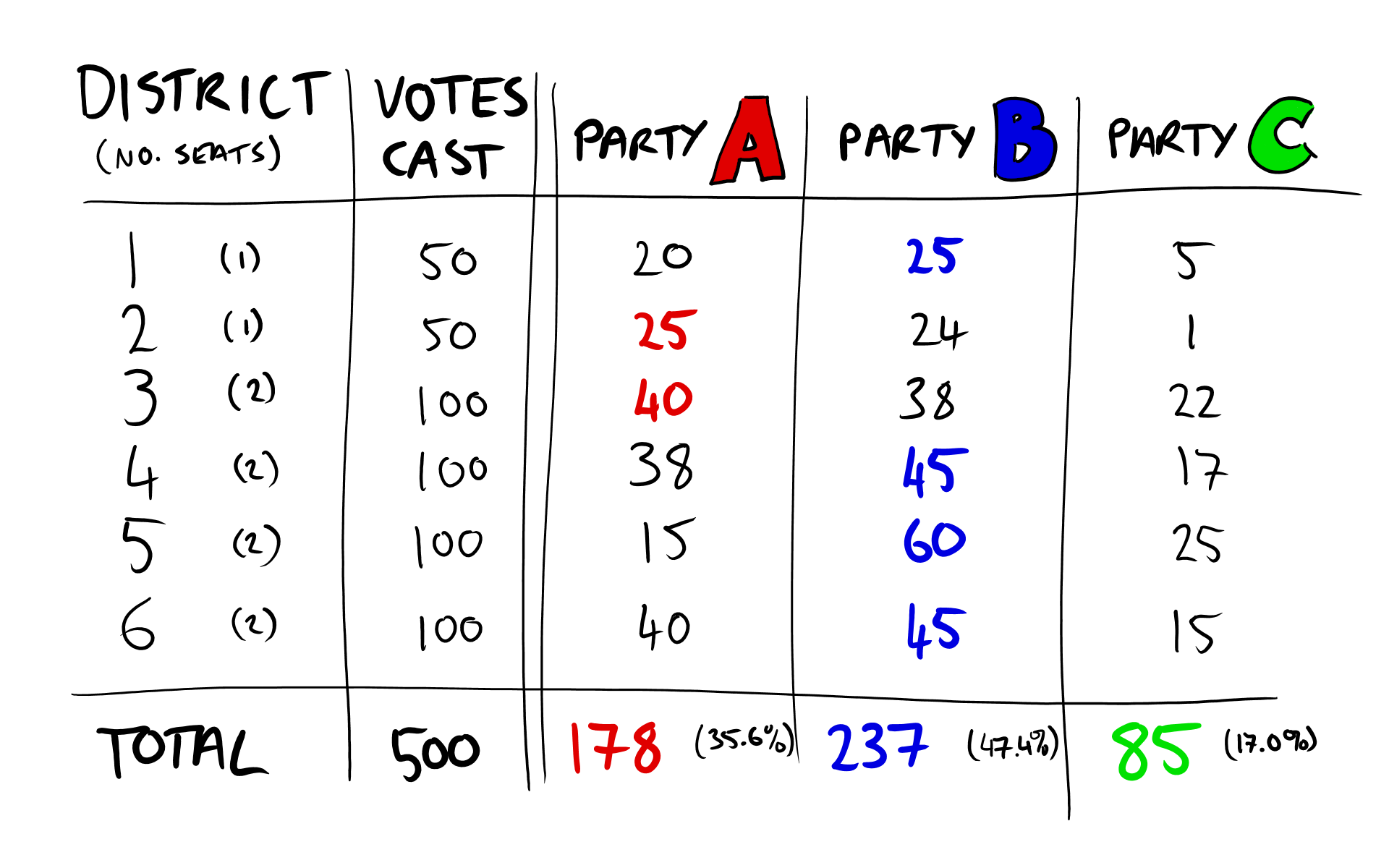
Those are some awfully slim majorities you’ve got there, it would be a shame if someone were to… mess with them.
After all the votes have been counted, the election overlords begin to run through the DMP algorithm.
Step 1: Calculate the proportional seat allocation.
This is simple enough, and uses the LR-Hare method. In the Proportionalian election, the breakdown looks like this:

Maybe in a different system party A’s share wouldn’t Droop so much…
Step 2: Award seats to plurality winners.
This is arguably even simpler, as it’s exactly the same as FPTP. The parties with the most votes win a seat for their primary candidate. In our case, party A has won districts 2 and 3, and party B has won the rest. In single-seat districts, that’s the end of it. In two-seat districts, there is still a seat to be won. If the winning party has a secondary candidate they are thrown back into the mix for the next stage, but with only half of the winner’s votes.
Step 3: Arrange remaining candidates by popularity.
At this point in FPTP, everyone without a seat would now be thrown into a bin marked ‘reject’. Not so here, as the remaining unfilled seats need to be filled, and they need to be filled by the most popular candidates possible. Each party’s unsuccessful (or secondary) candidates are arranged by percentage of the vote they received in their district. For example, party B’s list is:

I’m awfully sorry sir, I thought for a moment that you were two parliamentary candidates on each other’s shoulders in a trenchcoat.
Step 4: Proportionally fill remaining seats.
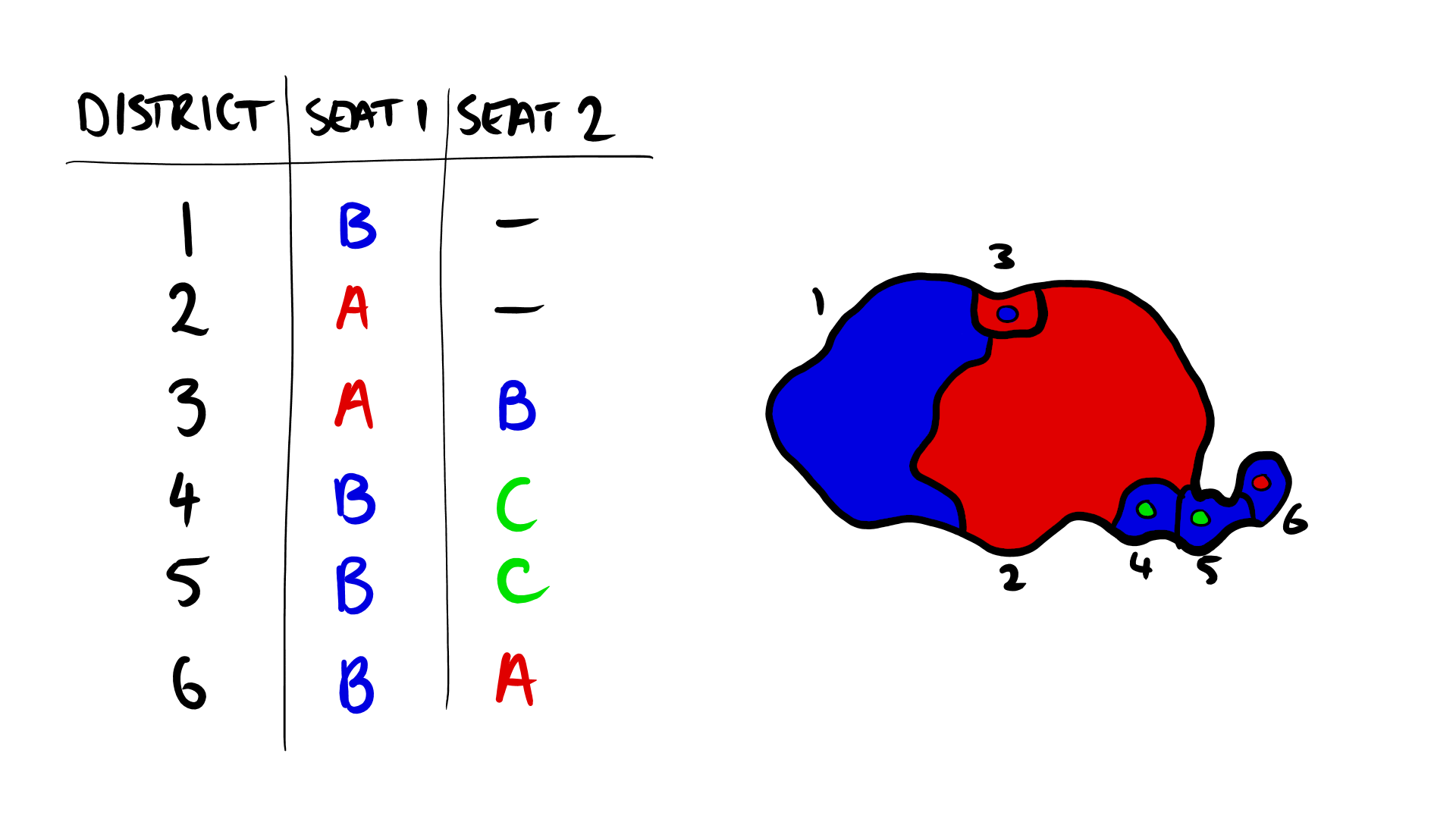
It’s what it says on the tin really. Party B has already won four seats in step 2, so their most popular candidate (district 3) is called upon to fill the second seat, and everything is sorted. But wait! One of party C’s candidates is also popular enough to be chosen to fill the seat.We have a challenger!
Step 5: Resolve conflicts.
In cases where two candidates are trying to fill one seat, the winner is picked by a bloody fight to the death the more locally popular candidate wins (in this case, party B’s candidate wins with 38% of the vote compared to party C’s 22%). The losing party then moves to the next candidate on their popularity list. This may cause conflicts elsewhere, so this step is repeated until all seats are filled.
There are no other conflicts in Proportionalia, so the final result is as follows:
It’s always good to have some green spaces in the city.
It’s all as simple as that! There are literally no awkward scenarios or real-world examples that can be discussed. Show’s over.
…
Oh of course the show’s not over. There are a whole raft of complications, such as where independent candidates fit in, what happens if a party runs out of candidates, what happens if a party wins too many seats etc. etc. All this and some juicy real-world simulations to come in subsequent installments.
Disclaimer & acknowledgement
As of now my sole source for detailed DMP information has been Wikipedia. I haven’t looked at the original paper describing the system, firstly because why read instructions when you could brute-force it yourself, and secondly because it runs to more than 80 pages. It is the work of one man, Sean Graham, who devised it while an undergraduate at the University of Alberta, reaching levels of nerdery some of us only dream of. Thanks, Sean!